When I look at math, I see pictures. While this is not a strictly neurological phenomenon like synesthesia, I suspect it is probably innate, in that not everyone sees math this way, and those of us who do cannot undo it, any more than a right-handed person can become left-handed. Neurologists have noted that people who are blind from birth, and consequently lack a visual representation of the world, tend to represent spatial relationships in algorithmic terms, like a recipe for navigating through spatial environments. Walk this far, turn left, five steps, turn right, reach upward. I have known many colleagues whose brains are built similarly, who internalize mathematics in an algorithmic rather than a visual way. For their brains, mathematical objects and relations are like parts of a machine that can be put together in various ways to create different objects with different functions, and an equation is like a beautiful, intricate clockwork toy. Most of us do a little of both, and perhaps the most gifted of all are the truly mathematically ambidextrous, who can shift at will between visual and algorithmic thinking, whichever is most suitable for a particular problem.

No branch of mathematical physics is a more natural fit to visual thinking than relativity, Einstein’s famous theory uniting space and time into a single, observer-dependent framework.  One reason relativity appeals to the visually inclined is that the clockwork mathematical machinery of relativity is notoriously complex. Einstein, when he proposed his equations for the general theory of relativity that supplanted Newtonian gravity, believed that the theory was too complicated for anyone to ever find an exact solution. He was wrong about this—Karl Schwarzschild derived the first exact solution to Einstein’s equation while a soldier on the Russian Front of World War I in 1915—but Einstein was mostly right in that such solutions even today are few, and highly idealized. Seeing the equations of relativity as pictures is immensely useful, because relativity recasts phenomena as diverse as gravity and time as manifestations of geometry. Einstein’s general theory of relativity, for example, reveals the force of gravity as an illusion generated by the curvature of space and time. Time itself in relativity is geometric, just another dimension like the three dimensions of space, all of which can be unified into a four-dimensional spacetime. The effects of relativity, such as the apparent slowing of time with motion, can be seen as aspects of the geometry of this higher-dimensional construction.

The equation expressing the length of a path—called the proper time—through four-dimensional spacetime is this:

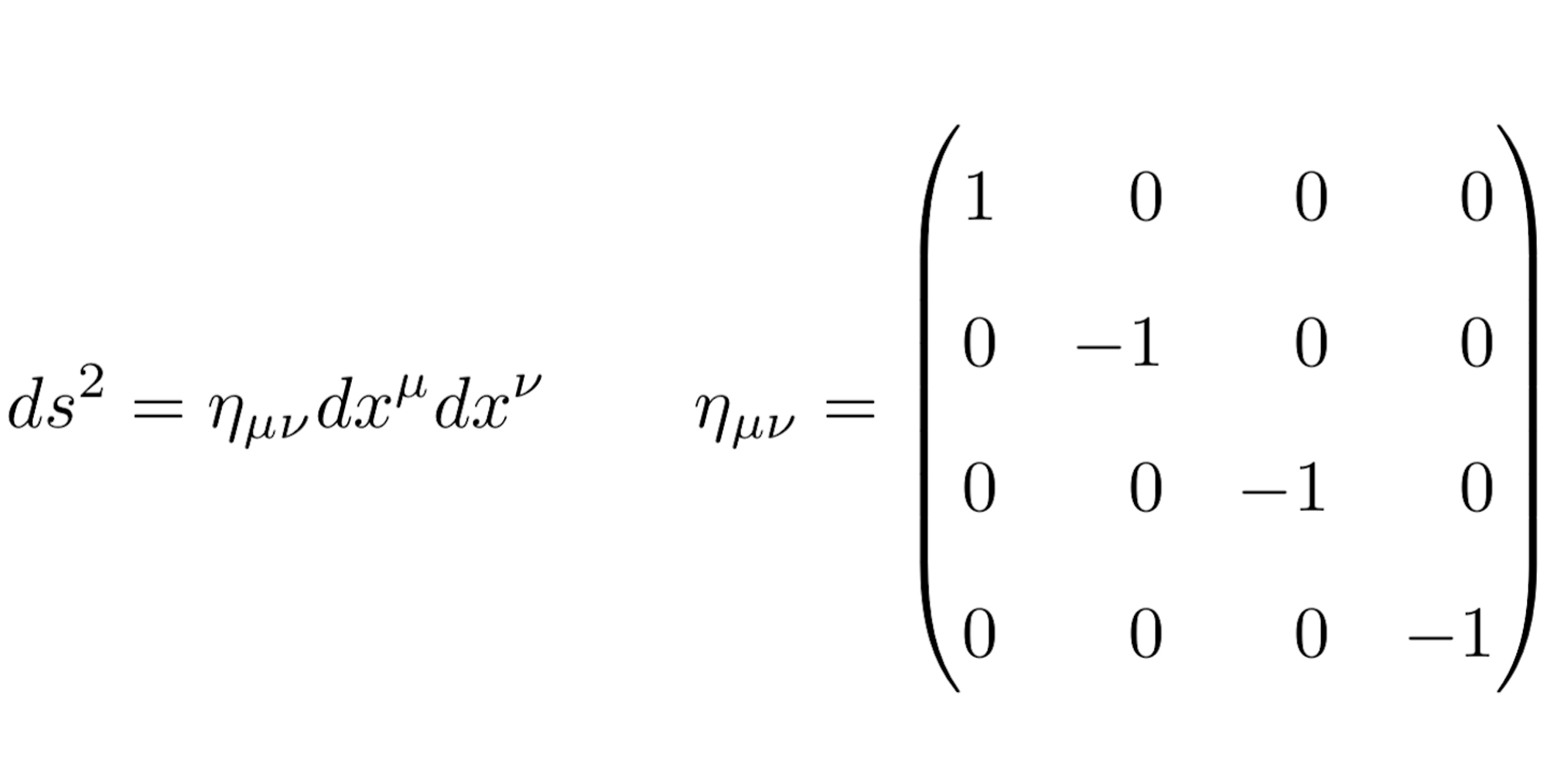
When I look at this equation, a picture appears in my mind. I’ve drawn that picture above. Let’s break this diagram down and explore its meaning. Since the human brain is not equipped to directly visualize more than three dimensions, we reduce the four-dimensions of spacetime to three, two dimensions of space and one of time, drawn here in perspective. In this picture, traveling horizontally moves you through space (labeled by x in the diagram), while progressing through time is represented as vertical motion (labeled by t). In this way we can visualize the unification of space and time: time is another direction, like north or east or down. The dimension of time is unique, because we can cease motion through space, but we cannot cease moving through time. You cannot choose to avoid the next second, although you can choose not to move north. The path of an observer through space and time is called a world line, and every observer moves from the past to the future at the same rate. You can neither speed up nor slow down, always moving from the bottom of the picture toward the top.

An observer who is stationary in space moves on an exactly vertical world line, and a moving observer travels along a curved world line, traveling through space but still always upward through time. A point along an observer’s world line, a moment in space and time, is called an event. Your life, seen in spacetime, is one such world line. Strung along that world line like beads on a necklace are the events of your life: birth, your first kiss, your marriage, your death. In relativity, all of these events exist together as different points in time and space.

Consider a single event in spacetime labeled on the picture by P. Let us say that this point in space and time represents the moment that a star explodes in a supernova. At the moment of the explosion, its light begins to travel outward into space. Light may be the fastest thing in the universe, but it really moves pretty slowly. Light moves 30 centimeters—about a foot—in one nanosecond, which is roughly the length of time it takes the chip in a cell phone to perform one calculation. The light emitted by the hypothetical supernova travels away in all directions, creating an expanding sphere in space, represented in the diagram as a circle which grows in diameter at the speed of light as it moves forward through time. If I measure time in nanoseconds and distances in feet (or time in years and distance in light years), light travels along a path tilted at a 45- degree angle on the diagram of spacetime. The expanding circle of light then sweeps out a conical shape, with the point of the cone at the event P—the moment of the supernova explosion. Since nothing can travel faster than light, nothing starting at P can travel outside this future light cone. This is causality represented as geometry: the causal future of the supernova is geometrically a region of space and time. Similarly, the supernova has a past light cone, defined by the world lines of incoming light and representing its causal past. The region of spacetime outside the past and future light cones of P is in neither the supernova’s causal past nor future, and is labeled ELSEWHERE. This is in a sense a separate universe: it is a region of space and time that has no cause-and-effect connection with anything that happens at the event P, because such a relationship would require travel faster than the speed of light. We are all trapped within our individual futures and pasts, which can overlap but never fully intersect, and our futures are fully as determined as our pasts.

The transformation of mathematics of relativity into a picture is a profoundly powerful tool. We can represent the mathematics of causal relationships as equivalent geometric relationships, and organize them in a clear and understandable way on a diagram of future and past light cones in spacetime. In so doing we change our internal picture of how the universe itself is structured, and the philosophical consequences are transformative. The universe of relativity is a deeply fatalistic picture of the nature of reality, a viewpoint which was embraced by Einstein. In an article for the New York Times Magazine in 1930 titled Religion and Science, he wrote “For any one who is pervaded with the sense of causal law in all that happens, who accepts in real earnest the assumption of causality, the idea of a Being who interferes with the sequence of events in the world is absolutely impossible! Neither the religion of fear nor the social-moral religion can have any hold on him.” Einstein, while rejecting the religious notion of an interventionist Being, nonetheless retained a notion of religious awe at the universe itself, writing in the same article: “I assert that the cosmic religious experience is the strongest and noblest driving force behind scientific research.” In a simple picture, we are granted the power to see the universe as Einstein did, and share in his awe. ♦