In October 1877, the Cincinnati Enquirer hosted a debate between two physics professors in Ohio over a broiling national controversy: Was there such a thing as a curveball?

Pitchers claimed they were throwing them, batters claimed they were missing them, and fans claimed they were seeing them, but a chorus of doubters argued that the “curved ball” was a physical and scientific impossibility. On one side of the Enquirer debate was Orange Nash Stoddard, a distinguished science professor at Wooster University, lovingly nicknamed the “Little Wizard” by students. On the other was Robert White McFarland, a mathematician and civil engineer at Ohio Agricultural, which we now know as Ohio State. Stoddard’s position: “There is no such thing.” McFarland’s: “There is a curve.”

At the end of the nineteenth century, baseball was rapidly professionalizing and growing in popularity. For many, its geometric diamond arrangement and the spectacular physics of bat and ball made it a truly scientific sport. In turn, fans, players, commentators, and even natural scientists used baseball to test theories about the natural world. How far could a hit ball travel? Could a thrown ball really curve? Although debates over the curve are known to fans and sports historians alike, they are usually understood in a narrative of progress: an old misperception of physics that inevitably gave way to scientific truth. But the curveball debate was more than that. It was an argument about the contours of our shared reality. Could baseballs really bend along their path, or was it all a collective delusion?

A century of debate about the curve shows how professional and amateur sports served as venues not only for entertainment but for knowledge production. Curving baseballs invited researchers to rethink their understanding of physics and test inherited theories against physical demonstration. In turn, the debates brought new understandings of physics to a reading and sporting public. Debating the curve was an opportunity to grapple with the complexity of our physical world. But the curve controversies were also about what it meant to live in that world, and particularly what it meant to be American; about truth and deception in public life. The very question of whether there is such a thing as a curveball revealed how our societies and our knowledge of the physical world evolve in constant dialogue.

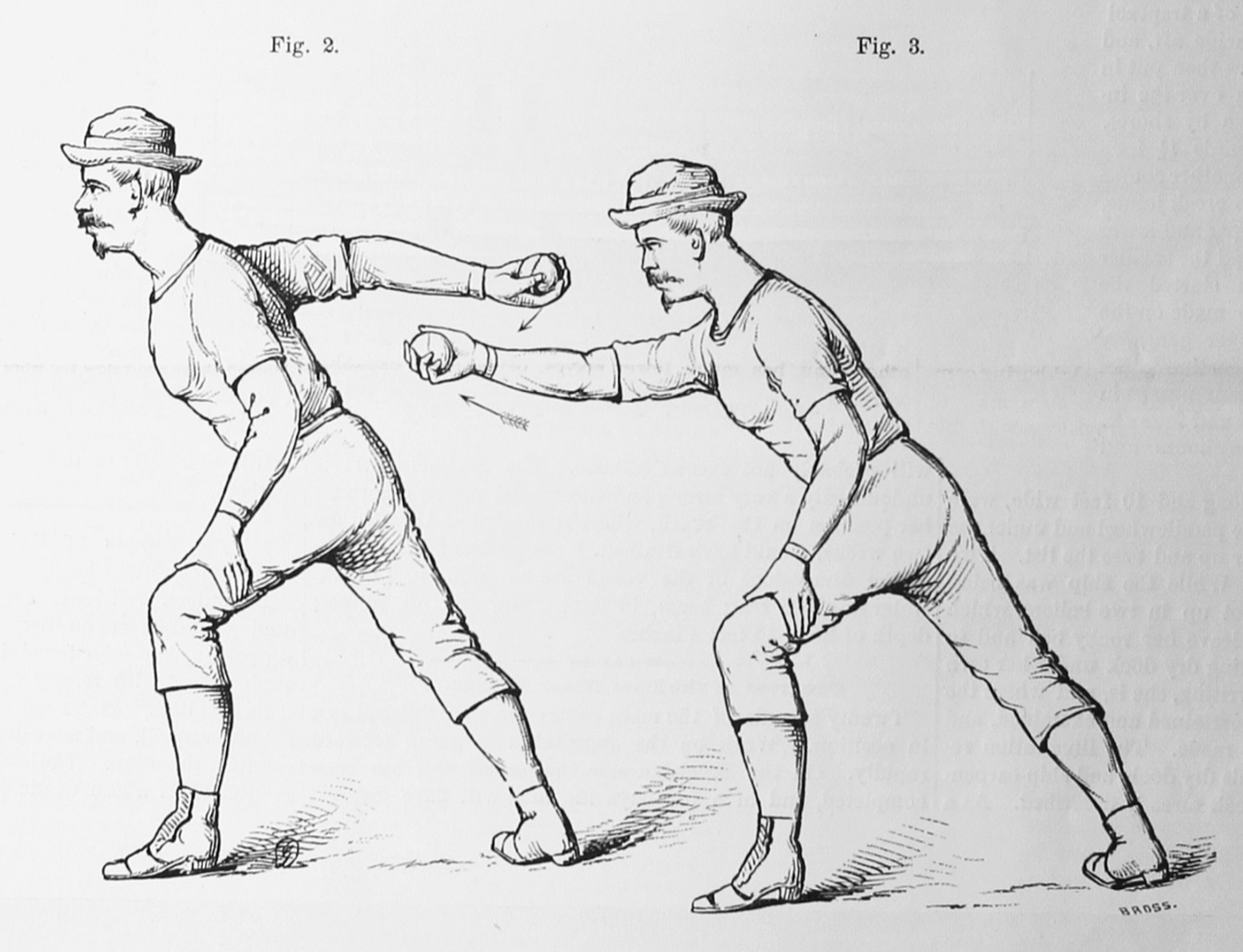
“Base Ball Science,” Scientific American 37, no. 20, November 17, 1877.

*

The first curveball is generally credited to William Arthur Cummings, a star of mid-nineteenth-century baseball, who earned the nickname “Candy” for his sweet mastery of the craft. Using an underhanded motion, Cummings twisted his hand as he released the ball, producing an initially straight pitch that curved away to the side as it reached home plate. He claimed his inspiration was the spiraling motion of tossed clamshells. In September 1875, his “peculiar inside-curving ball” was noted in coverage of a game between the professional squad from Hartford, Connecticut, that Cummings played for and an amateur team from Ludlow, Massachusetts. (The amateurs still won the game, the early equivalent of a local rec team defeating the Yankees.)

As other pitchers began to integrate Candy’s technique, newspaper discussion of “curved ball” pitching spread across the eastern U.S. In 1877, the Evansville Daily Courier of Indiana hailed a new local hurler who pitched “the popular ‘curved’ ball so swiftly that no one in the club was able to strike the balls.” After years of batters’ domination, curving balls rebalanced the scales back in the pitchers’ favor. Within a decade, the curveball was heralded as a revolution—“the greatest change ever introduced into the game,” according to an account from 1883, around the same time that Candy considered retiring to become a house painter.

How the curve worked, however, was initially a mystery. “Please tell me what a curved ball is in playing base-ball,” asked one Cincinnati Enquirer reader in May 1876. That August, another inquired, “What is meant by a curved ball—is it a pitch or an underhand throw, how does it curve, and can you explain how it is done, how the ball is held, etc.?” The curveball was, in the first place, a tactical curiosity for passionate fans and aspiring players. With many men eager to make a nickel on the new national pastime, mastering the pitch promised upward mobility. Yet as the Enquirer’s answers made clear, its exact mechanics were elusive: “A curved ball is one which leaves the hand in a straight line and just before it reaches the home plate suddenly curves out toward the end of the bat…. by a twist or twirl of the ball that can not well be described.” Commonality did not initially mean common understanding.

Originally an art to be mastered, the great curveballers were labeled “artists” for decades. But over time, the pragmatic matter of how to throw a curveball became a scientific problem: Was it even possible to do so? Spectators, after all, had witnessed balls that appeared to contradict the laws of motion. That all this might simply be trickery of the eye accorded with a widespread wariness in the late nineteenth century about fraud and deception. Newspapers of the era abounded with accounts of sleight-of-hand subterfuge: “Pepper’s ghost,” for instance, in which reflective glass panes made an off-stage ghost appear to float before theater audiences, wowed crowds from London to New Orleans. Magic was often just a trick of the eye.

“Why does a ball ‘curve?’” asked Columbus Ohio’s Dispatch in July 1876. Here was a question “our scientific heads can spend a deal of brain power in solution of.” While it was widely accepted that the “laws of motion” made a curving pitch impossible, the Dispatch conceded “it is a fact … that there is such a thing as curved balls. Every base-ballist knows it.” The everyday know-how of players seemed to trump the public understanding of science. Could it be, as one popular theory proposed, that the force of air against the ball slowed one rotating side more than the other and produced a curving motion? The Dispatch granted that “the thinking men among us may ferret out something more probable.” Debates continued: In July 1877, “several young men” wrote the Minneapolis Tribune that they were fully divided on whether it was possible to throw a curving ball. In September, a writer asked the Chicago Inter-Ocean to “Explain the philosophy that governs the curved ball as thrown by some of the professional baseball players of the United States, or as curved on a billiard table by scientific players.” People wanted not just to behold or even throw the curve themselves, but to understand how it could be possible in the first place.

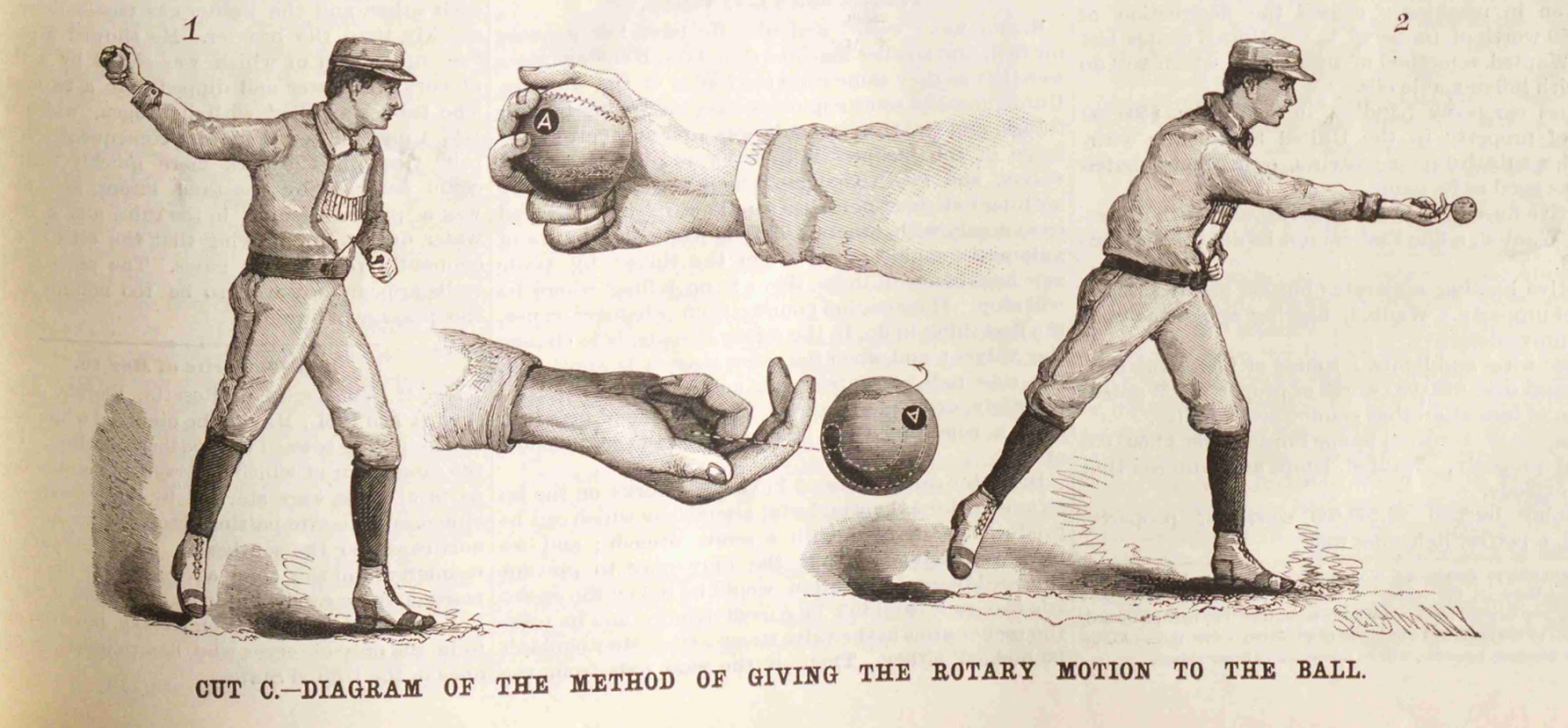
“The Art of Pitching in Baseball,” Scientific American 55, no. 5, July 31, 1886.

The Enquirer, finding the curve debate was good for business, decided to bring in experts to settle the matter: “The question of whether there is such a thing as a curved ball in pitching is dividing in opinion not only the patrons of the game, but also learned Professors and Doctors of Natural Sciences.” An unnamed resident of Cincinnati had even promised $1,000 (nearly $30,000 in today’s dollars) to any man who could demonstrate a true curve in controlled conditions.

For Orange Nash Stoddard, who “cheerfully” proffered his opinion on the subject, it was transparently obvious that a pitcher could not produce a curve. “That the hand can not affect the path of the ball after leaving it seems plain enough to those who are familiar with the laws which control the motion of matter,” he wrote. A late-breaking curve, Stoddard argued, would require some additional force on the ball during its flight. This was the essence of the physics of motion set down by Isaac Newton, and it applied to “the base-ball and the dust in the air, as well as the planets.” Believers in the curve, Stoddard suggested, were mistaking the performative spins and gesticulations of pitchers with the physics of their delivery.

McFarland rejected this illusion theory of the curve and was equally quick to dismiss a concurrent opinion that had appeared in Scientific American, which was “wrong all the time.” Unlike Stoddard, who argued from first principles, McFarland proposed a simple experiment: If the reader threw a large board forward while spinning it, they would notice a curving trajectory as the friction of the air seemed to exert a stronger force on one side of the board than the other. “Try it and see,” he urged, with a stone, disk, or anything else handy. “Whether the philosophy of it is right” was uncertain, McFarland cautioned, but the experiments demonstrated clearly that the curve existed. The debate between Stoddard and McFarland was, in other words, a question of whether immutable scientific laws theorized and passed down by great thinkers could be contradicted by experience.

*

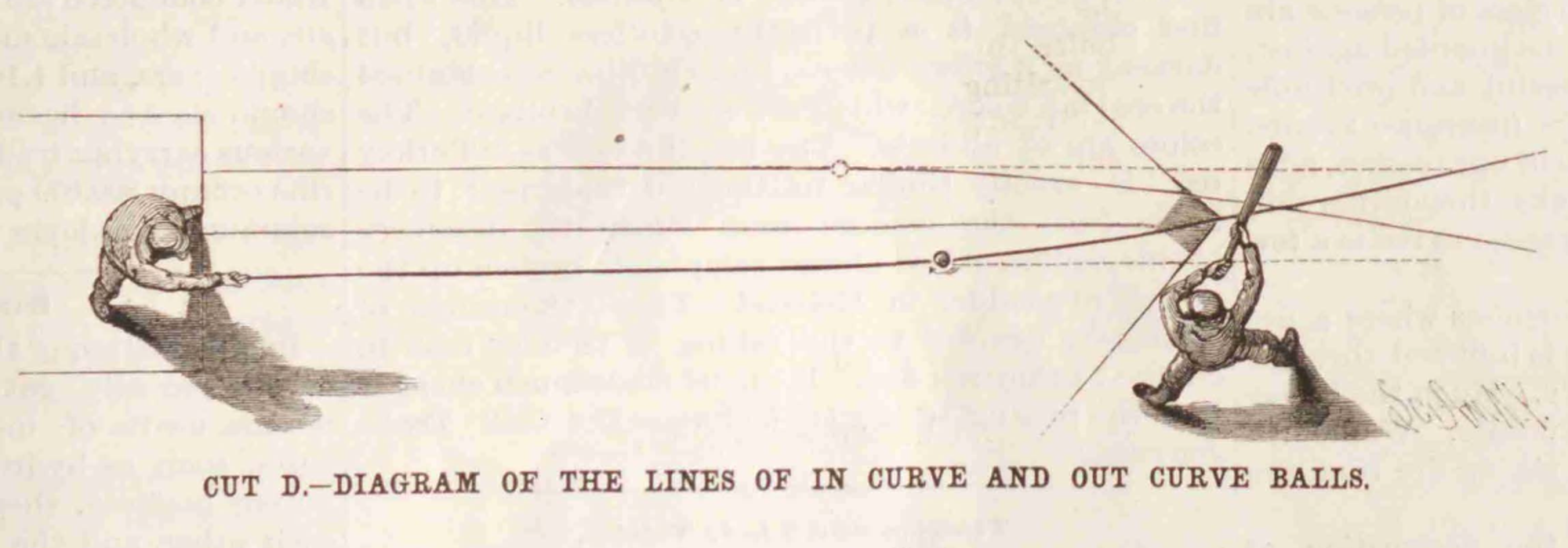
The Enquirer was unwilling to immediately side with one argument over the other, so a full demonstration was planned for October 21, 1877, when the Cincinnati Red Stockings played the visiting Boston Red Caps. After two innings of miserably muddy play, the game was paused so that Bobby Mitchell, a lefty from Cincinnati, and Tommy Bond, an Irish righty from Boston, could attempt to throw curving balls. “Infinitely more interesting than the game was the experiment,” explained the Cincinnati Gazette, which pitted “Disciples of Isaac Newton” against “Base ball scientists.” A chalk line running from home plate to first base was chosen as the test site, and Mitchell stood on one end of the line, facing one barrier erected about halfway along the balls’ path and a second barrier at the end. For his ball to reach the other side, it would need to bend around the first and then arc back to avoid the second.

“The Art of Pitching in Baseball,” Scientific American 55, no. 5, July 31, 1886.

The weather was “insufferably disagreeable,” and Bond struggled, at first, to get his ball to cooperate. Finally, he managed a pitch that “started fairly on the west side of the line, curved over to the east side to pass the first barrier, and back again to the west side to avoid the other barrier.” Bond had thrown an undeniable “curved” ball. Mitchell went next, the experiment flipped to account for his southpaw delivery, and after a series of attempts managed a perfect “meanderer” that curved around the barriers as well. That a righty and a lefty had both accomplished the feat demonstrated wind alone was not diverting the balls. The test was reported as a success and satisfied “nearly all who witnessed it that a curved ball is a reality, whatever theorists may say.”

Accounts of the Cincinnati exhibition rippled through nearly every major newspaper in the country, where it was often a front-page story. The trial was repeated the next day, and then again during the final game of the season—the public couldn’t get enough. Similar demonstrations cropped up in other states: A pitcher visiting Rochester, New York, demonstrated the curve there as well after astronomer Lewis Swift, best remembered for discovering 13 comets, insisted it was a physical impossibility. “College professors should not dispute with base-ballists in matters of science,” one newspaper snarked. The Cincinnati Enquirer was no less decisive in its appraisal of the showdown between “Science and Base-Ball”: “If Professor Stoddard … had been at the Cincinnati Base-Ball Ground Saturday … he would not have demanded a wait of 200 years for another Sir Isaac Newton to convince him it could be done. Mitchell of the Cincinnatis, or Bond of the Bostons, would have answered every purpose of Sir Isaac.” Swift, for his part, acknowledged his mistake and overconfidence: “I began to investigate the matter, and soon saw, that instead of being impossible, it was in accordance with the plainest principles of philosophy.” Baseball players had taken on the role of educators and experimentalists, making games into popular science.

If the demonstrations were convincing to those who saw them, their verdicts were not, in an era dominated by print media, immediately accepted by everyone. As late as 1885, Charles M. Schaefer, a self-professed “learned” gentleman and world traveler in Shelbyville, Indiana, wrote Cincinnati’s Commercial Tribune insisting that the curved ball was physically impossible—he was willing to journey to any demonstration and be thumped by such a ball if it did. After a test was arranged for October 6 in front of 800 Cincinnati fans, Schaefer was a conspicuous no-show. Yet the continuation of the debate revealed persistent fears of public deception: Americans were not the sort to believe a fable on authority. They needed to see the evidence for themselves.

*

We now know that the curving motion of a spherical object relies on a physical phenomenon called the Magnus effect, named for German physicist Gustav Magnus, who argued back in the early 1850s that rapidly rotating projectiles deviate from a straight path as they move through air. Isaac Newton had actually recognized that tennis balls could behave similarly, but his brief comment on the subject in 1672 escaped wider notice until the twentieth century. In 1877, the same year as the curved ball debates, the physicist John Strutt, who was known as Lord Rayleigh and later won a Nobel Prize, wrote a short article applying Magnus’ theory to the irregular movement of tennis balls. In 1904, as the American press started referring to “curveballs” as a distinct type of pitch, German physicist Ludwig Prandtl theorized the existence of a thin “boundary” layer around rotating objects, which influenced their movement and yielded anomalous deviations from their expected path.

That Rayleigh and Prandtl were both involved in early aerospace investigations reveals how “baseball science” was, in part, a matter of aerospace engineering. The wind tunnel test chambers that inspired Rayleigh and Prandtl would have been unknown to many generalist American scientists and educators of the late nineteenth century. Over time, however, some began to explore the curve question from this theoretical perspective. In 1879, mathematician and astronomer Henry Turner Eddy, later the president of the University of Cincinnati, published a paper exploring the “lateral deviation of spherical projectiles,” a phenomenon best known and most frequently observed “in pitching baseball.” Although it was commonly asserted that throwing a curving ball was scientifically impossible, Eddy sought to offer an explanation for the undeniable evidence of experience.

Importantly, it was baseball that encouraged American scientists and mathematicians like Eddy to think about the physics of curving balls. That Americans generally associated the phenomenon with baseball and billiards, rather than tennis, shows how local cultures of sport could shape the formulation of scientific questions. Magnus recognized the fundamentals without watching a single game, but many Americans needed to see it in person. Thus, beginning in 1877, Scientific American returned to the question multiple times: An article that year included multiple diagrams demonstrating how a curved pitch could be thrown and explained the underlying physics. But a follow-up in 1886, two years after the sport formally allowed overhand pitching, revealed how far understanding had advanced. Henry Chadwick, the writer who invented the sport’s box scores and penned its first rulebook, noted that pitching at the end of the century was not fundamentally different from earlier decades—many of the greats would still be highly effective hurlers. But one fundamental difference was “the horizontal curve of the ball through the air”; this innovation was “the great feature of the modern art of pitching.” Why and how the curve worked was obvious to Chadwick: The art was sustained by settled science. For the next few decades, being able to throw an effective curve partly determined your ceiling as a baseball pitcher, as an exceptionally curved ball became the norm.

*

It may seem surprising, then, that the curveball reemerged as the subject of existential quandary in the middle of the twentieth century. In May 1941, a man named R. W. Madden wrote in to The New Yorker to share the winding tale of a conversation held some years earlier with a part-time baseball scout. Over the course of a few draught beers on a relaxing hotel veranda in Flemington, New Jersey, discussing the encroaching threat of fascism in Europe, the former scout told Madden that Americans were not safe from collective delusion. In fact, their national pastime proved it: “No man alive, nor no man that ever lived, has ever thrown a curve ball,” the scout said. “It can’t be done.” Madden at first refused to believe it: He had been to games and seen curveballs. “Because you expect to see them,” the man responded, explaining that female fans rarely noticed the curve because they were untrained to expect it. Curveball belief, Madden explained, was a relic of “the mass American mind.”

A stream of responses followed the letter, with most focusing on the blasphemous rejection of settled science. A purported former classmate of “Eggy” Madden, Donald Larkin, claimed that Madden had always been a gullible sort. Ernest Kellogg found a 1911 copy of Albert Spalding’s America’s National Game, which presented McFarland, Stoddard, and Swift as participants in a single, outdated newspaper debate, already long settled by “reputable contemporary scientists.” Johns Hopkins physicist Robert Wood, a veteran of the original curve wars, wrote in to set the record straight with quotes from his own 1899 demonstration in the journal Science. Few, however, reckoned with the political overtones of Madden’s suggestively allegorical letter. If there was no such thing as the curveball, his story suggested, it revealed something fundamental about American public opinion. In contrast to the fear of deceptive showmen latent in earlier curve debates, Madden’s note positioned the existence of the curve as a metaphor for the susceptibility of modern mass society to fascist delusion. The one respondent who took up this thread—Ray Lillibridge, of New Haven—voiced hope for a scientific analysis, but concluded that “kidding ourselves that we can temporize with a united, capable, ruthless world-combination aligned against us put curve balls in the shade.” The vital matter was instead to “think straight about more important things.” Clear, linear logic to make sense of a disastrous, curving world.

In response to the reopened curve debate, Life magazine hired the celebrated photographer Gjon Mili to take high-speed images of a curveball thrown by Philadelphia Phillies pitcher Cy Blanton. “Baseball is founded on the premise of the curve ball,” Life’s article began, even as “the no-curve theory has always had a small group of backers.” Mili’s photographs track Blanton’s “curve” from an elevated angle and the batter’s perspective, a ghostly grey ball traveling just to the left of a straight white index line against a black, Eadweard Muybridge-inspired background. Blanton’s curve and his “screwball,” a pitch intended to twist in the opposite direction, looked indistinguishable. Baseballs were simply too heavy for a pitcher to impart a meaningful curve the way one might with a ping-pong ball, Life argued. The late, “breaking” motion of pitches was an artifact of the batter’s perspective: “What control a pitcher has over the ball is simply the ability to apply varying degrees of speed.” As the world raced rapidly to war, the curve was, once again, an “optical illusion.”

Life’s “demonstration,” which pitted scientifically framed photographs against the perceptual experience of players and fans, produced further waves of skeptical responses. Now, however, the situation was reversed from earlier debates: Physics suggested that a ball should curve on its path, so scientists set out again to demonstrate it. Frank Verwiebe, the author of a celebrated introductory physics textbook, arranged a test in Illinois that ultimately suggested Life had the issue half-right: A ball did curve, but the perceptual challenge of tracking a spinning, onrushing ball made minor movements appear more dramatic. World War II delayed further effort on the problem, but a second photographic study, this time from Look magazine in 1949, confirmed Verwiebe’s findings, suggesting that “a curve ball actually does curve.”

Life returned to the question in 1953, by which time baseball had acquired “a new television audience subject to strange new electronic illusions”—the curveball might just be one of them. In the decade since Mili’s first images, high-speed photography had seen dramatic improvements: Wartime researchers, for example, developed rotating mirror cameras capable of more than a million frames per second to capture the explosions of atomic bombs. Slow-motion video had also progressed, and the television show You Asked For It deployed new cameras to attempt to settle, with future Hall of Famer Bob Lemon, “baseball’s oldest argument.” The very foundations of an “objective” visual demonstration had shifted.

This time, Mili had Cincinnati Reds’ pitcher Ken Raffensberger throw a ball that was half-black and half-white on a pitch-black night, its rotations captured by rapidly flashing strobe cameras. Raffensberger’s curve, it turned out, moved at half the speed of a fastball—but spun very quickly, more rapidly than previously thought possible, at nearly 1,400 revolutions per minute (MLB data suggests today’s curves are closer to 2,500). Aeronautical engineer Joseph Bicknell, who helped develop the famous Wright Brothers Wind Tunnel at MIT, then tried to verify this initial data in his lab. Bicknell built upon contemporaneous studies by Igor Sikorsky and Ralph Lightfoot, two engineers with the United Aircraft Corporation, who had also used a wind tunnel to test the existence of the curve. The result in both cases was clear: “Yes, a curve ball does curve, but in a gentle arc.” The curve was real, even if the aerial zigzags imagined by earlier viewers were not.

*

Recent analysis suggests that curveballs have lost their former prominence in baseball. Play in the last few decades has been dominated instead by “sliders” and “splitters,” pitches of an intermediate speed with less of an extreme break than traditional curves. As Michael Baumann noted on FanGraphs in 2024, “Gen-Z is Killing the Curveball”: A disproportionate percentage of the declining number of curves thrown over the last five years have come from older pitchers. The curveball could join the Southern accent and alcohol industry as victims of Gen-Z’s cultural proclivities. But over a decade ago, sportswriter Malcolm Kelly had already claimed that curveballs were “slowly disappearing from the weapons rack of Major League Baseball.” Eulogies for the curve may be premature, but the pitch that once defined professionalism and art in baseball has certainly lost its centrality.

“Is there such a thing as a curveball?” was a persistent question for over a century. Some may still wonder. But the uniformity of its formulation masked ways that the “curve” itself was also changing, just like the technologies available to test it. The underhand curve of Candy Cummings and his ilk was gradually replaced by faster sidearm and overhand curves. Then, over time, these were overtaken by the 12–6 curve, made famous by Sandy Koufax, which moves in a largely straight trajectory but appears to break dramatically from the top of the clock to the bottom just as it reaches a batter. In Game 4 of the American League Championship Series this year, 40-year-old Blue Jays pitcher Max Scherzer “defied father time” to strike Randy Arozarena out with exactly such a curve for a crucial out.

The 12–6 curve actually “curves” very little, in the traditional sense, exhibiting less lateral movement than some “sliders.” Blanton’s curve for Life was a 12–6, which helps to explain why it had minimal lateral motion. “The curve” thus did not exist, in one sense, because it referred to a number of different approaches. That disambiguation might also explain why the metaphorical usage of “throwing a curveball,” in the sense of a disorienting social maneuver, only became part of popular vernacular in the latter half of the twentieth century. The curveball lost its art and became something anyone could do.

Scientists continued to study the physics of rotating baseballs, a sporting and intellectual problem that never fully lost its intrigue. In the late 1950s, Lyman Briggs, a lifelong baseball fan who had led the United States National Bureau of Standards during World War II, published one of the clearest wind tunnel analyses in the American Journal of Physics, confirming the findings of earlier curve supporters. Briggs had first studied the physics of baseballs during the war, when rubber shortages pushed the American and National Baseball Leagues to use balls with a cork interior. His follow-up study, like the analyses that preceded it, reveal how dramatic mid-century advances in aerospace engineering helped settle the scientific side of the curve debate. The same tools that allowed for the perfection of fighter jets helped to simulate the miraculous movements of curving balls.

What did it mean that the curveball existed? In 1911, Albert Spalding, of sporting goods fame, had argued that the early curve debates were “only interesting from historical and scientific standpoints, since every careful observer in the grandstand… is able to clearly note the very wide deflection given the ball by modern pitchers of every league.” It seemed that the overwhelming evidence of direct experience would always trump the claims of skeptics and sophists. But this ignores the centrality of trust in the creation and acceptance of scientific facts: A researcher must believe the evidence of another’s experiment and experience is valid and reliable, as Steven Shapin and a host of historians have shown.

When the curve debate reemerged in the 1940s, it also revealed that the controversy was always more than a simple question of fact. The existence of the curve was about what it meant to be American—whether one would be taken in by tricksters and frauds, fall prey to collective hysteria, or worse. Seeing was not always believing, it turned out, so theory and experiment were necessary to convince generations of skeptics that a pitcher really could produce magical movements in his throws, even if what they tossed was an illustrious amalgam of physics and optical illusion. Sports offered an improbable yet invigorating occasion for scientific experimentation and theoretical analysis: athletes as physics demonstrators, aerospace engineers as supporters, entertainment merged with public education. In another moment of political turmoil, it seems only right to have our facts straight about the curve. ♦