John Bell could hold a grudge. He’d been salty about quantum mechanics ever since he’d learned it as a college student in the late 1940s, in Belfast, Northern Ireland. Something seemed off about it, and he wanted to figure out what. Everyone—his teachers, his colleagues, even his textbooks—tried to dissuade him. They couldn’t.

Eventually, in 1964, Bell dug up an old debate that had exhausted both Albert Einstein and his contemporaries, dividing them over whether or not quantum mechanics—which describes the world of the very small—was a complete description of reality. Bell devised an experiment, easy enough to sketch on a blackboard but extremely difficult to perform, which could test the ideas at the center of the debate. When that experiment was finally done a few years later, its results were at once shocking and unsurprising. They confirmed that there are long-distance instantaneous correlations in nature, a possibility Einstein had dismissed as “spooky action at a distance.” For the most part, Einstein’s opponents hadn’t taken the idea seriously either. No wonder, given its strange and extraordinary implications. It’s as if two friends each took one of a pair of dice and traveled to opposite corners of the world, and then when one rolled her die and got a six, the other friend would be guaranteed to roll a six as well. Dice don’t do such things, of course, but microscopic particles such as electrons and photons of light can, and do, according to quantum theory.

Albert Einstein aired his concerns about quantum theory in a famous debate that began in the mid-1920s, when he locked intellectual horns with Niels Bohr, the great Danish physicist. Both men had played key roles in developing the theory, and Bohr was satisfied with it as it stood. But Einstein thought it was missing something crucial. While they agreed that quantum mechanics was brilliant at predicting the outcome of measurements, Einstein was unhappy with the theory’s inability to account for what was happening in the quantum world between measurements. Bohr didn’t mind. He thought this was as it should be—that the main purpose of scientific theories was to predict the outcomes of scientific experiments. To Einstein, this was a betrayal of the project of science itself. “Science,” he said, “has the sole purpose of determining what is.”

Out of sheer frustration, Einstein developed a series of thought experiments to show that Bohr was wrong, and quantum mechanics was missing important facts about the world. This culminated in a 1935 paper that Einstein co-authored with two colleagues, Boris Podolsky and Nathan Rosen, which came to be known as the EPR paper, after the authors’ last names. It pointed out that according to quantum physics, once two quantum objects interacted, they would become “entangled,” or connected in a manner that ensured later measurements made on both objects would be perfectly correlated, regardless of the distance between them. For example, say two appropriately entangled electrons are sent off in opposite directions. Their spins are measured along the up-down axis. Quantum mechanics demands that those spins will always be opposite. If one electron is measured to have spin up, the other will always have spin down, and vice versa. But quantum mechanics doesn’t tell you which electron’s spin will be up and which will be down—just that they’ll always be opposite.

To Einstein and his collaborators, this strongly suggested that the entangled electrons had opposite spins all along, and quantum mechanics was just incapable of saying what those spins were. Therefore, EPR argued, quantum mechanics gives an incomplete description of the state of the electrons in particular, and of quantum reality in general. The alternative explanation was mind-boggling: instantaneous long-distance connections between the electrons that ensured that their spins always mismatched when the measurements were made, no matter how far apart they were. Einstein thought this was obviously absurd. To him, the EPR thought experiment demonstrated that quantum mechanics was incomplete.

Bohr responded with a famously obscure reply, seemingly agreeing with Einstein that “spooky action at a distance” was impossible, but also denying the validity of the EPR argument. Despite his ambiguous take, Bohr was widely regarded as being probably correct. The debate itself entered the realm of philosophy.

Years later, when a young John Bell encountered quantum mechanics in school, he wasn’t satisfied with it. “I hesitated to think it was wrong,” he said, “but I knew it was rotten.” Like Einstein, Bell was dissatisfied with Bohr’s way of thinking about quantum physics. He stewed on it for over 15 years, and then, in 1964, on sabbatical from his research position at CERN near Geneva, Switzerland, he finally turned his attention to the old quantum debate.

Bell discovered that he could transform the philosophical question about Einstein’s “spooky action” into an experimental question. In the EPR thought experiment, there was perfect correlation between the two electrons—but only if their spins were measured along the same axis. If their spins were measured along different axes—say one along the vertical axis and the other along an axis halfway between vertical and horizontal—quantum mechanics predicted an imperfect correlation between the two. And for certain angles between those axes, the correlation was larger than could be explained without an instantaneous, long-distance connection between them. In short, Bell had shown that EPR was only half-right: the choice wasn’t between spooky action and quantum mechanics being incomplete. The choice was between spooky action and quantum mechanics being incorrect. Quantum mechanics predicted instantaneous long-distance correlations. Could the prediction actually be upheld in the laboratory?

Bell’s paper, published in an obscure short-lived journal, didn’t garner much attention at first. But in 1972, results of the first test of Bell’s theorem, conducted by John Clauser and Stuart Freedman at the University of California, Berkeley, were published. They measured the polarization of photons (a property of the particles akin to spin), rather than the spins of electrons, but the idea was the same and the results were clear: they agreed with quantum mechanics. Other teams mostly confirmed the results. But in all of these experiments, the decisions about the measurements—for example, the choice of the axes along which to test the photon’s polarization—were made before the two photons left their source, leaving open the possibility that some signal was passing between the two ends of the experiment no faster than the speed of light, coordinating the responses of the photons to the polarization measurement devices.

Then in 1982, Alain Aspect and his team at the Institut d’Optique in France published the results of a more definitive but trickier experiment.

In the picture above, Bell, who had encouraged both Clauser and Aspect to perform their experiments, has sketched a diagram of Aspect’s experiment, conducted earlier that year. The photons leave the central hub and fly out to opposite ends of the experiment—about a foot apart, the distance light travels in a billionth of a second, as Bell has indicated in the diagram. There, a switch sends each photon to one of two polarizers, which measures its polarization in one of two directions. The results of the polarization measurements are recorded. Crucially, in Aspect’s experiment, the decision to send a photon one way or the other is made after the photons are already zipping in opposite directions, to eliminate the possibility that any signal traveling even at the speed of light could make it from one photon switch to the other. One switch should not know what the other switch did.

The equation Bell wrote above the diagram is a version of his theorem:

Bell's inequalities.Courtesy of the author.

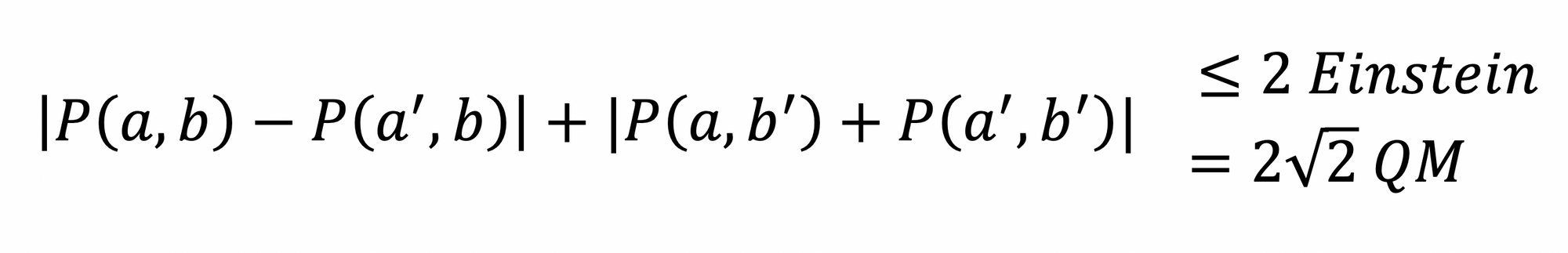
It lays out the range of possible correlations if the polarizations are determined in advance, as Einstein would have liked, as well as the correlation predicted by quantum mechanics, which lies outside that range. In other words, if an experiment returns 2 or less, Einstein was right; if it returns 2√2, then quantum mechanics is correct. Aspect’s experiment observed the latter. Again, the results were unambiguous: “spooky action at a distance” is real in the quantum world.

Bell’s work, and that of Clauser, Aspect, and those who followed, led to what Aspect later called “the second quantum revolution.” The most obvious outcome of that revolution today is the burgeoning industry of quantum computing. Entanglement also underpins quantum cryptography and quantum networks. Without Bell’s willingness to look in dark corners of physics others had abandoned, those fields might not exist as they do today.

Although he agreed that Clauser’s and Aspect’s experiments proved that Einstein’s preferred solution to the question of entanglement was impossible, Bell still thought that Einstein was more right than Bohr: there was something about quantum mechanics in general, and its long-range correlations in particular, that needed a clear explanation. “I felt that Einstein’s intellectual superiority over Bohr, in this instance, was enormous,” Bell said, “a vast gulf between the man who saw clearly what was needed, and the obscurantist.” Also, Bell did not agree that his proof—or any proof—had ruled out alternative ideas, despite Bohr's insistence that quantum mechanics needs no further elucidation. “What is proved by impossibility proofs,” he said, “is lack of imagination.”

Decades later, this fundamental concern about quantum mechanics remains unresolved. ♦